【なにはさておき量子論 第3章 ハイゼンベルクの不確定性原理】
目次へ 次へ進む 前へ戻る

P.ラプラス
正直に告白しておこう。人物中心の量子論を展開しようと決意したのだが、人物のエピソードをひろってゆく作業というのは、実はあまり創造力を必要としない。思い切って言ってしまうと、いろいろな文献をカンニングして文章を作っている気持ちになって来る。しかしこればかりは、自分で考えていても書けるものではないし...
これは、私にとって、フラストレーションだったのである。
しかし、この章からは違う。もちろん人物中心であることは止めない。だが、創造力を発揮できる場所にさしかかっているのだ。なんてったって、章のタイトルが「不確定性原理」で、項のタイトルが「ラプラスの悪魔」だもの。
さて、不確定性原理という、いわゆる量子論の革命的原理を話し出す前に、”ラプラス”が、18世紀に考えた悪魔を紹介しておこう。ただし、悪魔と言っても邪悪な存在を意味する者ではない。
ラプラスという人は、ナポレオン時代のフランスの数学者である。しかし、政治の分野にも天分があったらしく、ナポレオン皇帝の内相までつとめたそうである(わずか六週間であったそうだが)。こんなエピソードがある。
あるときナポレオンがラプラスに言った。「おまえの書いた本は大層有名だそうだが、神のことがどこにも出てこないではないか。」 ラプラスは、こう答えた。「陛下、私には、神という仮説は不要なのです。」
この発言は、今でこそ、あまりインパクトがないかもしれないが、18世紀のヨーロッパでこれを言ったのは、実は大変なことだ。不遜とも言えるほどで、神を仮説と呼んだ彼の意地が伺える。
「数学とは、物理学を解くための道具である。」と豪語したのも彼である。
(この意見には、ひそかに私も拍手を送っている。)
ビリヤードの台の上を転がる玉を考えてもらいたい。ある瞬間に、玉が台の上のどこにいて、どちらへどのくらいの速さで動いているのかがわかれば、その先の玉の動きは予測できる。
もし、摩擦がなく、空気抵抗もなく、玉は台のへりで、完全弾性衝突(速さが変わらない衝突)をすると考えると、その玉のこれからの動きは完全に計算できる。それが、数分後であれ、数万年後であれ、玉の位置と動きは予測可能だ。ばかばかしいから誰も何万年も先の玉の動きなど計算してみないだけである。
そして、玉が複数個になっても事情は同じだ。玉と玉との衝突という要素が加わるだけで、いかに玉の数が多くなろうと、計算が増えるだけで、予測という事実については、全く完全である。
異論は? 無いね。
さて、ここで話を飛躍させるが、ビリヤードの玉を、この宇宙の全ての原子にあてはめたらどうなるか? 数が多すぎて話にならん、と思った人、今書いた、ビリヤードの例を思い出してほしい。文字通り、天文学的な数になるであろうが、原理的には、ビリヤードの玉と同じ事ではないか? もし、この瞬間の宇宙全部の原子の位置と速度(速さ+方向)がわかれば、全ての未来は予測可能なことにならないか。
それができるスーパーマンを、ラプラスは悪魔と呼んだ。
確かに人間業ではない。それは認めよう。しかし、仮想の超人「ラプラスの悪魔」なら、原理的には、それができるはずなのである。宇宙といえども、人間といえども、所詮多数の原子と原子の相互作用で運動している。ラプラスの悪魔には、現在の全ての原子の状態がわかっている。従って、全ての未来はお見通しである。
我々が、人間の意思で決めたと思っていることでも、実はそれも脳内原子の相互作用の結果なのであり、それをも予測できるのがラプラスの悪魔なのである。
こうなると、人間の自由意思というものも実は、悪魔の手のひらの上、ということになる。(この意味でこの超人は「悪魔」と呼ばれたのだろう。)
ラプラスの悪魔には、某という人が、明日どんなことを考え、何をするか、ということも、某という島国が、200年後にどうなっているのかも、この宇宙が、500億年後にまだ存在しているのかも、全てわかっているのである。
さて、どう思うだろうか?
次項では、「不確定性原理」に突入する前段の話をする。余談に見えるかもしれないがそうではない。心して読んでいただきたい。
一言いいたい!

【なにはさておき量子論 第3章 ハイゼンベルクの不確定性原理】
目次へ 次へ進む 前へ戻る


ガリレオ・ガリレイと彼の作った温度計
2.測定すると...
「測定」という行為を考えてみよう。何も難しい事ではない。
今、目の前に、1リットルの水があるとする。「温度を測定しなさい。」と言われたら、みなさんは何をするだろうか。
すぐ近くに温度計がなければ、まずそれを調達するだろう。東急ハンズにでも行けば、ちょうどいい温度計が見つかるはずである。
余談
温度計という言葉は正しいのだろうか、温度は「計る」ものだろうか? それとも「測る」ものだろうか? いや「量る」ってのもあるぞ。自分的には、「測る」が正しいと思うのだが温度計とか体重計とか、「計」の字が登場するのは変な気がする。
余談ついでに
世界で初めて温度計を作った人は誰か知っている? どうも、かの”ガリレオ”であるらしい。ただし、温度を測る必要に迫られて作成したものではなく、一種の装飾品に近いものだった。(写真参照)外気温の変化で水中の気球状の物体が浮いたり沈んだりする。現在でも充分鑑賞に堪えうる装飾品ではないかと思う。
閑話休題
さて、温度を測ろう。簡単である。温度計を水に突っ込んで、目盛りを読めばよい。$21.3℃$とか$16.7℃$とか、読むことができれば測定完了である。
その水の温度は、$21.3℃$なり、$16.7℃$と報告すればいい。
本当にそうだろうか?
次の例を考えてみよう。
$1cc$($1m\ell$)の水がある。「温度を測定しなさい。」と言われたら、さっきと同じ方法で本当にいいのだろうか?(図7参照)

$1cc$といえば、一辺$1cm$の立方体である。仮に、$0℃$、つまりほとんど凍る寸前の水があるとして、そこに、常温(まあ$20℃$くらいだろう)の温度計を突っ込んだら、$0℃$と測定されると思うか?
普通の棒状温度計を$1cc$の水に突っ込めば、温度計が水に浸る部分が水の容量に比べて大きすぎないか。だとすれば、温度計そののものが持つ温度によって、$1cc$の水は熱をもらい、温度計の目盛りは、$10℃$くらいを示すのではないか、ということは容易に想像がつく。
そこから類推すれば、$1000cc$($1\ell$)の水だって、温度計そのものの温度によって変えられた温度が測られると言えないだろうか? ごく微量で影響はない、と言えばそれまでだが、厳密には温度計によって外乱された温度が測定されるはずである。
言い換えてみよう。
はじめから、温度計の温度を水と同じにしておけばいいではないか、という人へ、それならば、いったい何のために温度を測るのか?
同様なことがいかなる量を測定する場合にも当てはまるのである。
例えば、電流を測定することを考える。その場合、電流計を回路に直列に入れる。電流計とは、極めて電気抵抗が小さく回路を流れる電流に影響を及ぼさないように設計されている。しかし、電流計の針を振らせるという仕事をするのに抵抗ゼロ(電力ゼロ)では不可能である。従って、電流系を入れることによって回路の抵抗は変わり、測定される電流値も電流計によって外乱された数値になる。
今度は電圧を測定することを考える。この場合は、電圧計を回路に並列に入れる。電圧計は、極めて電気抵抗が大きく、極微弱な電流しか流れないように設計されている。しかし、極微弱でも電流は流れてしまう(というより、極微弱な電流が流れないと、電圧は測定不能だ)。従って、電圧計によって外乱された電圧しか測定できない。
という話をしても、まだ首をかしげている人がいるはずである。そもそも何が言いたいの? という疑問だと思う。
そこで、話を量子論の世界へ持って行く。
電子の運動状態を測定してみよう、という話である。
電子の状態を測定する、とは何のことか?
前項で話した、ビリヤードの玉を思い出してほしい。玉の未来を予測するためには、現在の何の値が必要であったかを思い出していただけばよい。それは
「速度」は二つの値(方向+速さ)になるぞ、と思った人はいるかな? 実は、速度のように向きと量を持ったものを、「ベクトル」という。高校数学を思い出そう。矢印で、向きをあらわし、その長さで量をあらわすものである。速度は、典型的なベクトル量である。
確認しておこう。物体の現在の位置と速度がわかれば、ラプラスの悪魔には、その未来が予言できるのであった。従って、電子であろうとも、今現在の位置と、速度がわかれば、それが電子存在のための(力学的)条件を満たしているということだ。
加速度はどうなっている?と考えた人、素晴らしい。でもその人にはこう言おう。
物質は、なにかと相互作用しない限り、その速度を変えることはないのだ。すなわち外部からなんらかの力が働かない場合は、加速度は生じない。もし仮に加速度が生じているとすれば、それは別の物質と相互作用をしていることになる。
よって一個の電子の(力学的)状態を言い表すには、位置と速度を測定すればよい。
さて、それでは、電子の位置と速度をどうやって測定するのか?
一言いいたい!

【なにはさておき量子論 第3章 ハイゼンベルクの不確定性原理】
目次へ 次へ進む 前へ戻る

W.ハイゼンベルク
3.不確定の思考実験
一般的に、物の存在を確認するとき、私たちは何をしているのかを考えよう。
難しいことを言っているのではない。
光(太陽からだったり、蛍光灯からだったり、裸電球からだったり)が、物に当たって反射してきたものを目が捉えて、それがそこにある、と認識しているのである。
つまり、我々は、光を媒介として、ものを認識している。
電子を認識するときもこれと同じと考えてよい。但し、位置を正確に知ろうと思うと問題がある。
光とは何であったかを、再度確認する。
何度も書いてきたことだが、光が電磁波という波であることは、マックスウェルの電磁方程式によって確認されたのであった。その後、アインシュタインの光電効果、プランクの前期量子論により、光が粒子としての性質も持つこともわかってきたが、とりあえず、光は、波動としての性質を持つことは確かなことなのである。
光でものを見るときには、その物体の大きさより小さな波長を持った電磁波でないとものの位置はわからない。光が物体により反射されて、観測装置(例えば目)によって認識されるときには、光の波長以下の精度の位置はわからないのである。波の性質として波長より小さい物質で、波は反射せず、素通りしてしまうからだ。
もうひとつ、顕微鏡等の観測装置を通して物の位置を認識するとき、その分解能をあげるためには、レンズの直径を大きくしなければならない。レンズの直径が大きいほど、鮮明な影像が得られるという事である。(カメラのレンズや、天体望遠鏡を考えれば納得できるだろう。)
電子の位置を「正確に知る」ためには、波長の短い電磁波が必要なのである。従って、かなり波長の短いガンマ線でないと、電子の居場所を、正確に知ることはできない。というより、原理的には、波長を短くすればするほど、電子の位置をより正確に知ることができるのである。
そして、電子に当たったガンマ線がどのように観測されるかを、図8で見てほしい。
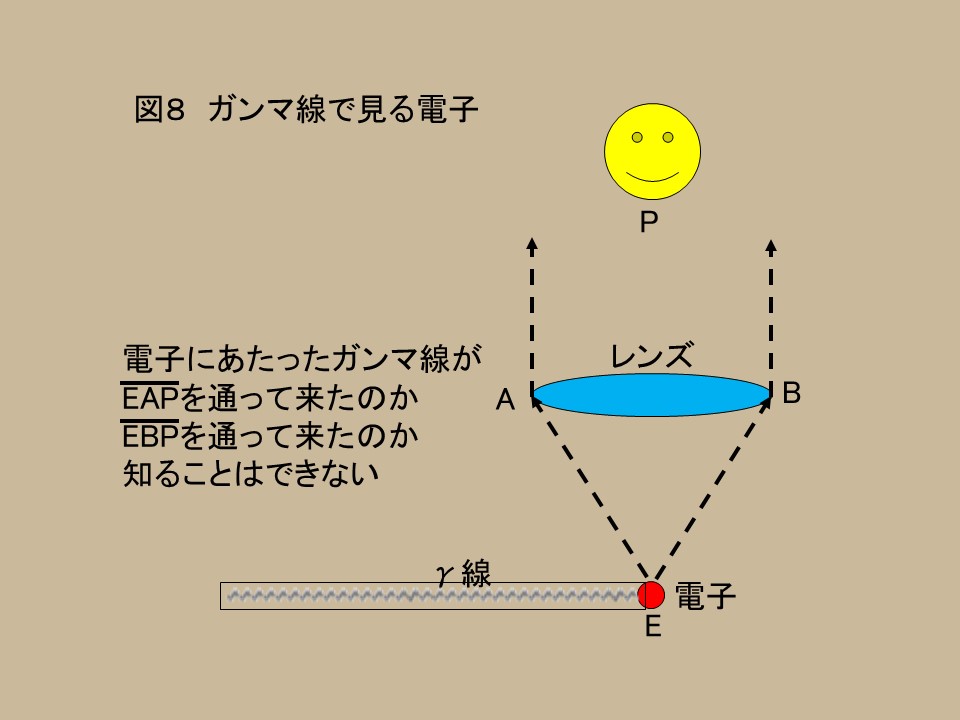
ガンマ線は電子にあたって反射(散乱)され、そのガンマ線を見る(測定する)ためには、顕微鏡同様レンズを使用しなければならないが、ガンマ線は図の、EAPを通って来るのか、EBPを通って来るのか(それともその中間あたりを通るのか)は、ガンマ線が波である限りわからないのである。
ここまでは、よいだろうか。
次の問題である。それは、光に運動量があるということである。
よって、ガンマ線も運動量を持つので、EAPを通った方がEBPを通るより電子を右に強く蹴ることになる。ガンマ線はどこを通ってくるのかわからないのだから、ガンマ線は電子を強くも弱くも蹴ることになる。
ガンマ線の波長を小さくするほど、ガンマ線の運動量は大きくなる。そして、レンズの幅を大きくするほど分解能が良くなり、電子の位置ははっきりする。ところが、運動量が大きいほど、レンズの幅を大きくするほど、ガンマ線が電子を蹴る運動量がわからなくなり、蹴られた電子がどこへ飛んで行くかわからなくなる。
長々と話してきたが、以上が、”ハイゼンベルク”が行った思考実験である。
勘違いしないでほしい。位置と運動量を掛けた値が、$h/4\pi$以上になると言っているのではない。
「位置の不確定さ」と「運動量の不確定さ」を掛けたものが$h/4\pi$以上になるのだということ。これは、$\Delta x$も$\Delta p$もゼロにはなれないと言っているのだ。だって両者の積がある数値(ゼロではない)より大きいのだから。
つまり、
これは、実験の精度の問題ではない。物質に関する根元的な問題である。だから「不確定性原理」という。
測定という行為が実際の状態を攪乱する、という実験的事実を深く掘り下げてみると、観測以前に、物理量は不確定であるという根源的な事実を突きつけられた。
ここに一つのパラダイムシフトがあることを理解して欲しい。つまり、観測前の電子には、ある決まった「位置」や「運動量」がある、とは言えなくなってしまったことだ。なぜなら観測しても、それ以前の状態を「原理的に」知ることができないのだから、電子は、ある瞬間に決まった「位置」「運動量」を持つということ自体検証不可能だから。
これは、「決定論」の否定である。いかなる物質(粒子)も、ある瞬間の決定された「位置」と「運動量」を持たない。ならば、どんなに超人的な能力を持った「悪魔」であっても、これから先の状態を決定することが「原理的に」不可能になる。ここに、ラプラスの悪魔はその存在を否定されるしかないことになった。
一言いいたい!

【なにはさておき量子論 第3章 ハイゼンベルクの不確定性原理】
目次へ 次へ進む 前へ戻る


光は粒子だ 電子は波だ
A.アインシュタイン ド・ブロイ
4.「粒子」と「波動」の意味
前期量子論とは何であったか?
そう、プランクが示したエネルギーの不連続。ボーアが証明した電子軌道の不連続。我々は、不連続なものを相手にしている、ということであった。ド・ブロイによって、電子波が発見され、それは、電子に限ったことではなく、あらゆる物質は、粒子と波動、両方の性質を持っていることも、示されたのだった。
ここに颯爽と登場したハイゼンベルクは、「不確定性原理」を言い出した。奇異に感じた人はいないだろうか?
前期量子論と不確定性原理には、何の関連があるの? それを今回は説明する。それは、「粒子」と「波動」の意味を理解することでもある。
不確定原理とは、
$\Delta{x}$は、位置の不確定の幅を示す。
$\Delta{p}$は、運動量の不確定の幅を示す。(速度の不確定と考えてもよい)
ここで、$\Delta{x}$を限りなく$0$に近づけてみよう。すると、
つまり、位置だけを確定させるということは、物質の粒子性を表現することになる。
これに対し、$\Delta{p}$を限りなく$0$に近づけてみる。
よって、運動量だけを確定させるということは、物質の波動性を表現することになる。
よろしいか、つまり不確定性原理は、物質の究極の姿は、位置と運動量のどちらを正確に測るかによって、粒子だったり、波動だったりする、ということを言っている。
はい、プランク → ボーア → ハイゼンベルクとつながったね。
次に、($h/4\pi$)を考えてみよう。
もし、($h=0$)だったら、そもそも不確定性原理が意味を持たない。($\Delta{x}$)も($\Delta{p}$)もゼロでかまわない。従って、自然界は、連続であり、とびとびにはならない。
もし、($h/4\pi=100$)だったら、
もし、$1kg$の石が運動しているのを私たちが見たらどうなるか?
では、実際にはなぜこんなことになっていないか? それは、($h$)が非常に小さいからである。
再度、復習しておこう。($h$)をプランク定数といい、その値は、
相対論において、光速度が、私たちの日常の速度に対してあまりにも大きかったため、私たちは、相対論効果を日常で感じることはできなかった。
同様に、プランク定数が、私たちの日常物質の位置や速度に対して、あまりにも小さいので、私たちは、量子論効果を通常感じることはない。
例えば、さきほどの例で、$1kg$の石の位置を、$1mm$の$1000$分の$1$($1{\mu}m$:ほとんど私たちには見分けることができないほど小さい)の範囲で不確定であるとしても、その運動量は、$5.272859{\times}10^{-32}$$kg・m/$秒の範囲で不確定になっているはずで、こんな小さな速度のぶれなど、誰にもわからない。
でも、極微の世界では、そうは言っていられない。
意味のない計算をしていると思うだろうが、最後に出てきた速度($\Delta{v}$)は、実は、原子核の電荷がぎりぎり、電子をつなぎ止めておけるくらいの速度の不確定さなのである。
言い換えれば、原子の大きさより高い精度で電子の場所を確定させると、運動量の不確定さのため、電子は、原子から離れてどこかへ飛んで行く、ということになる。
つまり、電子は、原子の大きさ程度に位置が不確定でないと、原子の周りに存在できない。
なに、よく意味がわからん? 普通の人ならそれで正常。
電子は、原子の周りに存在する限り、原子の大きさ程度に位置が不確定になる、すなわち、電子は、原子核の周りに、まんべんなく存在しなければならない。よって、長岡半太郎が示した惑星モデルがここで破綻する。
電子は、原子核の周りに、もわーっと、雲のように存在することになる。
一言いいたい!

【なにはさておき量子論 第3章 ハイゼンベルクの不確定性原理】
目次へ 次へ進む 前へ戻る

チマローザ(の若い頃)
5.もう一つの不確定
ここまで、「なにはさておき量子論」を読み進めてくださった寛大なあなたにひとつ提案をする。
もし、「わかっても相対論」を読んでいないなら、ここで一旦、量子論を離れて、「わかっても相対論」を読んでいただきたい。全部とは言わない。第3章『質量はエネルギーである』まで、読破してもらいたい。なぜこんな提案をするかというと、「四元物理量」を知らない人が読んでも、この項がよくわからない恐れがあるからだ。いや、わかるように書いてもいいのだが、感動が薄れると言った方がいいかもしれない。
さて、ここにたどり着いたあなたは、四元物理量がなんであるかわかったとして、話を進める。
四元位置とは、何であったか?
さて、感動する準備はできたかな?
この四元物理量は、アインシュタインが「特殊相対性理論」の中で提唱したものである。それは、空間と時間を平等に扱ったら出てくる概念であった。従って量子論とは無関係のはずだ。私だってそれはわかっている。ところが面白いことが起こる。
前項までで書いた「位置と運動量の間には不確定の関係がある」を、四元物理量に中に見つけてみよう。
「位置」とは、空間上の場所である。前項までは代表して($\Delta{x}$)だけを書いてきたが、本来は
($\Delta{x},\Delta{y},\Delta{z}$)と表記するものだったのである。では運動量は? これも前項までは、($\Delta{p}$)で代表させて来たが、運動量はベクトルなので、方向成分を持つから、やはり($\Delta{p_x},\Delta{p_y},\Delta{p_z}$)と書くべきものであった。
よって、位置と運動量の不確定は、下記のように記述すべきものであった。
では、四番目の物理量だって、不確定になるだろう、と考えてみたらどうなるか? 光速度($c$)は定数であるゆえ、
感動した?
これは、”チマローザ”が発見した。(わーい!私も量子論研究者の仲間入り。しかし当然、これが新発見であるわけもない。実は、位置と運動量、時間とエネルギーは「正準関係」にある、と言われ、量子論の計算(量子力学)では重要なものなのである。
本当は、次のような証明をするのが一般的。
今、自分胸あたりの深さの海の中に立って、波を見ているとする。波は、高い状態と低い状態があるから、一番低いときはへそのあたりで、高いときは首のあたりまで来るかもしれない。でもとにかく波がひと揺れしないことには、振動数($1$秒間に何回揺れるか)は、わからない。あたりまえ。この振動数を($\nu$)として、それを観測するのに必要な時間幅を($\Delta{t}$)とする。
そして、第2章『ボーアの量子条件』の1.項『生みの親から育ての親へ』に出てきた
さて、いったい時間とエネルギーの不確定って、いったいなんだろう。
一言いいたい!

【なにはさておき量子論 第3章 ハイゼンベルクの不確定性原理】
目次へ 次へ進む 前へ戻る

ゼノン
前項では、「時間」と「エネルギー」が不確定の関係にあることを見てきた。
この項ではその意味を考えてみよう。多分、前項を読んだだけでは、
まず最初に、エネルギーを確定させることを考えよう。
原子物理学では、エネルギーを正確に決めることが求められる。実は、今までにそんな話をいくつもしてきているのである。
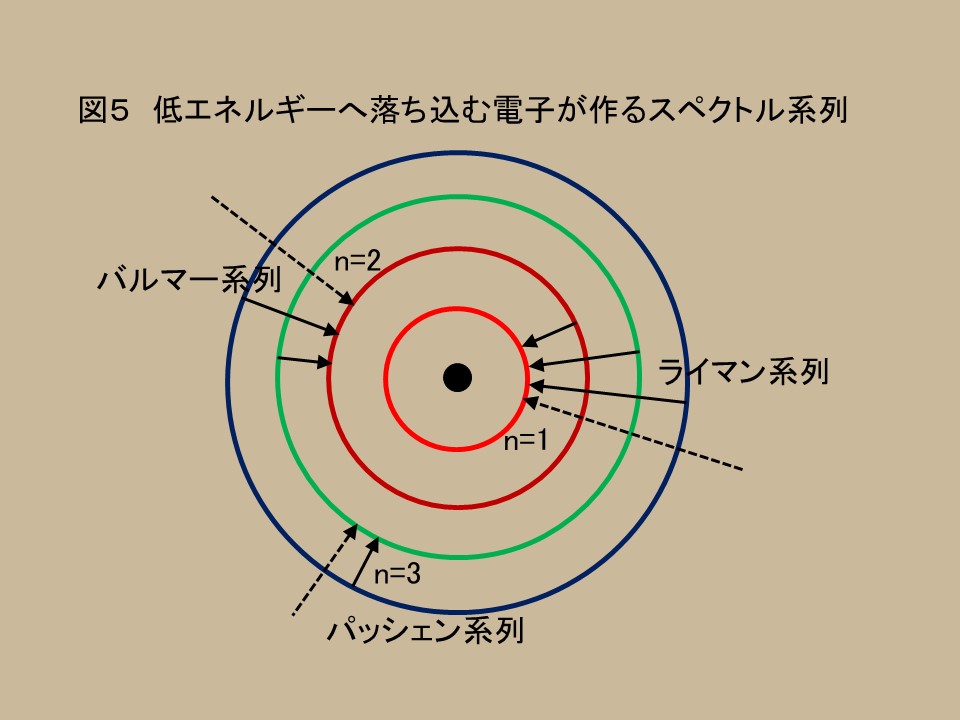
例えば、水素原子から、光が飛びだして来る値が、光を粒子と考えると、バルマー系列やライマン系列のように、エネルギーがとびとびになる、ということが言えたのは、当然、エネルギーが確定していたからである。
 【再掲】
【再掲】
エネルギーが確定していたということは、($\Delta{E}=0$)である(エネルギーの不確定要素がゼロなのだから)。ということは、不確定性原理を適用すれば、($\Delta{t}=\infty$)ということになる。さて、時間の不確定が無限大っていったい何?
簡単である。いつでも、エネルギーが確定しているということである。
これを、「定常状態」にある物質、という言い方をする。ある意味で、量子論の問題を解こうとするときには、対象物を「定常状態」である、としてエネルギーの方を決めてやることが多い。
では逆に、($\Delta{t}=0$)で、($\Delta{E}=\infty$)ということがあるか?
あるのだ。
極々、短時間($\Delta{t}\space{\fallingdotseq}\space0$)であれば、エネルギーの幅がとてつもなく大きく($\Delta{E}\space{\fallingdotseq}\space\infty$)なってもいいということだ。
($\space{\fallingdotseq}\space$)という歯切れの悪い記号を用いたことは許してもらいたい。私にも($\Delta{t}=0$)という状態(?)は想像できないのだ。ただ、次のようなことが考えられるだけである。
ちょっと寄り道をする。
($\Delta{t}=0$)は、『文学的』に言う「ある瞬間」というものと同義である。なぜ『文学的』かって? だって『物理的』に想像できないんだもの。なんとなく、全てのものが止まった世界を考えることができるだけである。そうであるとすれば、その『文学的』世界では、多分($\Delta{x}=0$)が言える。つまり、あらゆる物質が静止した世界だ。
いかなるものも動いていない。動いていないものに対して速度(どちらの方向へどのくらいの速さで動いているか)が定義できるか? 速度の定義から言って自己矛盾だろう。だってその物体は動いていないのだから。
「”ゼノン”のパラドックス」というのを知っているだろうか? 実はふたつあるのだが、今回はそのひとつを紹介する。(と言っても多分みなさんご存じだろう。)それは、「飛んでいる矢は止まっている」というものだ。
さあ、どう解決する?(ちなみにゼノンが考えたもうひとつのパラドックスを「アキレスと亀」のパラドックスという。こっちの方が有名かな? 「アキレスと亀」の話は、『問わず語り』にアップしている。)
つまり極限まで突き詰めると、静止してしまう物質はないのだ。粒子の位置($\Delta x$)を限りなくゼロに近づけても、矢は、運動量($\Delta p$)を持つ。点ではなく、何となく進行方向に少し延びている(ように私は思う)。
だから、「位置」と「運動量」の不確定は、「時間」と「エネルギー」の不確定と同じだ(と私は考えている)。直感的には、このように言った方がわかりやすいと思う。
「真空の揺らぎ」という現象がある。ある、と言い切るところから話をはじめると本当はルール違反である。
なのでこう書く。
つまり真空という、一見何もない空間でも、極々短い時間では、物質(と反物質)が生まれては消える、という現象があらゆる場所で起こってもよい。「真空の揺らぎ」によって、発生している(であろう)物質を、「仮想粒子」という。
ここで、次の疑問を持った人はいないだろうか?
ところが、「仮想粒子」が仮想でなくなることがあるのだ。
次章へ 一言いいたい!

目次へ 次へ進む 前へ戻る

P.ラプラス
正直に告白しておこう。人物中心の量子論を展開しようと決意したのだが、人物のエピソードをひろってゆく作業というのは、実はあまり創造力を必要としない。思い切って言ってしまうと、いろいろな文献をカンニングして文章を作っている気持ちになって来る。しかしこればかりは、自分で考えていても書けるものではないし...
これは、私にとって、フラストレーションだったのである。
しかし、この章からは違う。もちろん人物中心であることは止めない。だが、創造力を発揮できる場所にさしかかっているのだ。なんてったって、章のタイトルが「不確定性原理」で、項のタイトルが「ラプラスの悪魔」だもの。
さて、不確定性原理という、いわゆる量子論の革命的原理を話し出す前に、”ラプラス”が、18世紀に考えた悪魔を紹介しておこう。ただし、悪魔と言っても邪悪な存在を意味する者ではない。
ラプラスという人は、ナポレオン時代のフランスの数学者である。しかし、政治の分野にも天分があったらしく、ナポレオン皇帝の内相までつとめたそうである(わずか六週間であったそうだが)。こんなエピソードがある。
あるときナポレオンがラプラスに言った。「おまえの書いた本は大層有名だそうだが、神のことがどこにも出てこないではないか。」 ラプラスは、こう答えた。「陛下、私には、神という仮説は不要なのです。」
この発言は、今でこそ、あまりインパクトがないかもしれないが、18世紀のヨーロッパでこれを言ったのは、実は大変なことだ。不遜とも言えるほどで、神を仮説と呼んだ彼の意地が伺える。
「数学とは、物理学を解くための道具である。」と豪語したのも彼である。
(この意見には、ひそかに私も拍手を送っている。)
ビリヤードの台の上を転がる玉を考えてもらいたい。ある瞬間に、玉が台の上のどこにいて、どちらへどのくらいの速さで動いているのかがわかれば、その先の玉の動きは予測できる。
もし、摩擦がなく、空気抵抗もなく、玉は台のへりで、完全弾性衝突(速さが変わらない衝突)をすると考えると、その玉のこれからの動きは完全に計算できる。それが、数分後であれ、数万年後であれ、玉の位置と動きは予測可能だ。ばかばかしいから誰も何万年も先の玉の動きなど計算してみないだけである。
そして、玉が複数個になっても事情は同じだ。玉と玉との衝突という要素が加わるだけで、いかに玉の数が多くなろうと、計算が増えるだけで、予測という事実については、全く完全である。
異論は? 無いね。
さて、ここで話を飛躍させるが、ビリヤードの玉を、この宇宙の全ての原子にあてはめたらどうなるか? 数が多すぎて話にならん、と思った人、今書いた、ビリヤードの例を思い出してほしい。文字通り、天文学的な数になるであろうが、原理的には、ビリヤードの玉と同じ事ではないか? もし、この瞬間の宇宙全部の原子の位置と速度(速さ+方向)がわかれば、全ての未来は予測可能なことにならないか。
それができるスーパーマンを、ラプラスは悪魔と呼んだ。
確かに人間業ではない。それは認めよう。しかし、仮想の超人「ラプラスの悪魔」なら、原理的には、それができるはずなのである。宇宙といえども、人間といえども、所詮多数の原子と原子の相互作用で運動している。ラプラスの悪魔には、現在の全ての原子の状態がわかっている。従って、全ての未来はお見通しである。
我々が、人間の意思で決めたと思っていることでも、実はそれも脳内原子の相互作用の結果なのであり、それをも予測できるのがラプラスの悪魔なのである。
こうなると、人間の自由意思というものも実は、悪魔の手のひらの上、ということになる。(この意味でこの超人は「悪魔」と呼ばれたのだろう。)
ラプラスの悪魔には、某という人が、明日どんなことを考え、何をするか、ということも、某という島国が、200年後にどうなっているのかも、この宇宙が、500億年後にまだ存在しているのかも、全てわかっているのである。
さて、どう思うだろうか?
次項では、「不確定性原理」に突入する前段の話をする。余談に見えるかもしれないがそうではない。心して読んでいただきたい。
一言いいたい!

【なにはさておき量子論 第3章 ハイゼンベルクの不確定性原理】
目次へ 次へ進む 前へ戻る


2.測定すると...
「測定」という行為を考えてみよう。何も難しい事ではない。
今、目の前に、1リットルの水があるとする。「温度を測定しなさい。」と言われたら、みなさんは何をするだろうか。
すぐ近くに温度計がなければ、まずそれを調達するだろう。東急ハンズにでも行けば、ちょうどいい温度計が見つかるはずである。
余談
温度計という言葉は正しいのだろうか、温度は「計る」ものだろうか? それとも「測る」ものだろうか? いや「量る」ってのもあるぞ。自分的には、「測る」が正しいと思うのだが温度計とか体重計とか、「計」の字が登場するのは変な気がする。
余談ついでに
世界で初めて温度計を作った人は誰か知っている? どうも、かの”ガリレオ”であるらしい。ただし、温度を測る必要に迫られて作成したものではなく、一種の装飾品に近いものだった。(写真参照)外気温の変化で水中の気球状の物体が浮いたり沈んだりする。現在でも充分鑑賞に堪えうる装飾品ではないかと思う。
閑話休題
さて、温度を測ろう。簡単である。温度計を水に突っ込んで、目盛りを読めばよい。$21.3℃$とか$16.7℃$とか、読むことができれば測定完了である。
その水の温度は、$21.3℃$なり、$16.7℃$と報告すればいい。
本当にそうだろうか?
次の例を考えてみよう。
$1cc$($1m\ell$)の水がある。「温度を測定しなさい。」と言われたら、さっきと同じ方法で本当にいいのだろうか?(図7参照)

$1cc$といえば、一辺$1cm$の立方体である。仮に、$0℃$、つまりほとんど凍る寸前の水があるとして、そこに、常温(まあ$20℃$くらいだろう)の温度計を突っ込んだら、$0℃$と測定されると思うか?
普通の棒状温度計を$1cc$の水に突っ込めば、温度計が水に浸る部分が水の容量に比べて大きすぎないか。だとすれば、温度計そののものが持つ温度によって、$1cc$の水は熱をもらい、温度計の目盛りは、$10℃$くらいを示すのではないか、ということは容易に想像がつく。
そこから類推すれば、$1000cc$($1\ell$)の水だって、温度計そのものの温度によって変えられた温度が測られると言えないだろうか? ごく微量で影響はない、と言えばそれまでだが、厳密には温度計によって外乱された温度が測定されるはずである。
言い換えてみよう。
温度を測定する、という行為は、測られるものの温度を変えてしまう。ということである。つまり真に正確な温度を測定することはできない。
はじめから、温度計の温度を水と同じにしておけばいいではないか、という人へ、それならば、いったい何のために温度を測るのか?
同様なことがいかなる量を測定する場合にも当てはまるのである。
例えば、電流を測定することを考える。その場合、電流計を回路に直列に入れる。電流計とは、極めて電気抵抗が小さく回路を流れる電流に影響を及ぼさないように設計されている。しかし、電流計の針を振らせるという仕事をするのに抵抗ゼロ(電力ゼロ)では不可能である。従って、電流系を入れることによって回路の抵抗は変わり、測定される電流値も電流計によって外乱された数値になる。
今度は電圧を測定することを考える。この場合は、電圧計を回路に並列に入れる。電圧計は、極めて電気抵抗が大きく、極微弱な電流しか流れないように設計されている。しかし、極微弱でも電流は流れてしまう(というより、極微弱な電流が流れないと、電圧は測定不能だ)。従って、電圧計によって外乱された電圧しか測定できない。
という話をしても、まだ首をかしげている人がいるはずである。そもそも何が言いたいの? という疑問だと思う。
そこで、話を量子論の世界へ持って行く。
電子の運動状態を測定してみよう、という話である。
電子の状態を測定する、とは何のことか?
前項で話した、ビリヤードの玉を思い出してほしい。玉の未来を予測するためには、現在の何の値が必要であったかを思い出していただけばよい。それは
(1)位置(玉が今どこにいるか)が、わかればよいのであった。
(2)速度(玉がどちらの方向へどのくらいの速さで動いているか)
「速度」は二つの値(方向+速さ)になるぞ、と思った人はいるかな? 実は、速度のように向きと量を持ったものを、「ベクトル」という。高校数学を思い出そう。矢印で、向きをあらわし、その長さで量をあらわすものである。速度は、典型的なベクトル量である。
確認しておこう。物体の現在の位置と速度がわかれば、ラプラスの悪魔には、その未来が予言できるのであった。従って、電子であろうとも、今現在の位置と、速度がわかれば、それが電子存在のための(力学的)条件を満たしているということだ。
加速度はどうなっている?と考えた人、素晴らしい。でもその人にはこう言おう。
物質は、なにかと相互作用しない限り、その速度を変えることはないのだ。すなわち外部からなんらかの力が働かない場合は、加速度は生じない。もし仮に加速度が生じているとすれば、それは別の物質と相互作用をしていることになる。
よって一個の電子の(力学的)状態を言い表すには、位置と速度を測定すればよい。
さて、それでは、電子の位置と速度をどうやって測定するのか?
一言いいたい!

【なにはさておき量子論 第3章 ハイゼンベルクの不確定性原理】
目次へ 次へ進む 前へ戻る

3.不確定の思考実験
一般的に、物の存在を確認するとき、私たちは何をしているのかを考えよう。
難しいことを言っているのではない。
光(太陽からだったり、蛍光灯からだったり、裸電球からだったり)が、物に当たって反射してきたものを目が捉えて、それがそこにある、と認識しているのである。
つまり、我々は、光を媒介として、ものを認識している。
電子を認識するときもこれと同じと考えてよい。但し、位置を正確に知ろうと思うと問題がある。
光とは何であったかを、再度確認する。
何度も書いてきたことだが、光が電磁波という波であることは、マックスウェルの電磁方程式によって確認されたのであった。その後、アインシュタインの光電効果、プランクの前期量子論により、光が粒子としての性質も持つこともわかってきたが、とりあえず、光は、波動としての性質を持つことは確かなことなのである。
光でものを見るときには、その物体の大きさより小さな波長を持った電磁波でないとものの位置はわからない。光が物体により反射されて、観測装置(例えば目)によって認識されるときには、光の波長以下の精度の位置はわからないのである。波の性質として波長より小さい物質で、波は反射せず、素通りしてしまうからだ。
もうひとつ、顕微鏡等の観測装置を通して物の位置を認識するとき、その分解能をあげるためには、レンズの直径を大きくしなければならない。レンズの直径が大きいほど、鮮明な影像が得られるという事である。(カメラのレンズや、天体望遠鏡を考えれば納得できるだろう。)
電子の位置を「正確に知る」ためには、波長の短い電磁波が必要なのである。従って、かなり波長の短いガンマ線でないと、電子の居場所を、正確に知ることはできない。というより、原理的には、波長を短くすればするほど、電子の位置をより正確に知ることができるのである。
そして、電子に当たったガンマ線がどのように観測されるかを、図8で見てほしい。

ガンマ線は電子にあたって反射(散乱)され、そのガンマ線を見る(測定する)ためには、顕微鏡同様レンズを使用しなければならないが、ガンマ線は図の、EAPを通って来るのか、EBPを通って来るのか(それともその中間あたりを通るのか)は、ガンマ線が波である限りわからないのである。
ここまでは、よいだろうか。
次の問題である。それは、光に運動量があるということである。
よって、ガンマ線も運動量を持つので、EAPを通った方がEBPを通るより電子を右に強く蹴ることになる。ガンマ線はどこを通ってくるのかわからないのだから、ガンマ線は電子を強くも弱くも蹴ることになる。
ガンマ線の波長を小さくするほど、ガンマ線の運動量は大きくなる。そして、レンズの幅を大きくするほど分解能が良くなり、電子の位置ははっきりする。ところが、運動量が大きいほど、レンズの幅を大きくするほど、ガンマ線が電子を蹴る運動量がわからなくなり、蹴られた電子がどこへ飛んで行くかわからなくなる。
長々と話してきたが、以上が、”ハイゼンベルク”が行った思考実験である。
電子の位置をはっきり知ろうとすると、電子がどんな速度で動き出すかわからなくなる。この位置のわからなさを($\Delta{x}$)で表し、運動量のわからなさを($\Delta{p}$)で表すと、
電子の動き出す速度を小さくしようと思えば、電子の位置がわからなくなる。
$\Delta{x}\times\Delta{p}\geqq h/4\pi$であることを、ハイゼンベルクは証明した。($h$は、プランク定数である。)当然、プランク定数を$4\pi$で割ったものも定数である。つまり、$\Delta x$と$\Delta p$との積は、ある定数より小さくはなれないことを、式は示している。
勘違いしないでほしい。位置と運動量を掛けた値が、$h/4\pi$以上になると言っているのではない。
「位置の不確定さ」と「運動量の不確定さ」を掛けたものが$h/4\pi$以上になるのだということ。これは、$\Delta x$も$\Delta p$もゼロにはなれないと言っているのだ。だって両者の積がある数値(ゼロではない)より大きいのだから。
つまり、
電子の位置を正確に知ろう($\Delta{x}=0$)とすれば、その運動量はなくなる($\Delta{p}=\infty$)ということだ。
電子の運動量を正確に知ろう($\Delta{p}=0$)とすれば、その位置はなくなる($\Delta{x}=\infty$)
これは、実験の精度の問題ではない。物質に関する根元的な問題である。だから「不確定性原理」という。
測定という行為が実際の状態を攪乱する、という実験的事実を深く掘り下げてみると、観測以前に、物理量は不確定であるという根源的な事実を突きつけられた。
ここに一つのパラダイムシフトがあることを理解して欲しい。つまり、観測前の電子には、ある決まった「位置」や「運動量」がある、とは言えなくなってしまったことだ。なぜなら観測しても、それ以前の状態を「原理的に」知ることができないのだから、電子は、ある瞬間に決まった「位置」「運動量」を持つということ自体検証不可能だから。
これは、「決定論」の否定である。いかなる物質(粒子)も、ある瞬間の決定された「位置」と「運動量」を持たない。ならば、どんなに超人的な能力を持った「悪魔」であっても、これから先の状態を決定することが「原理的に」不可能になる。ここに、ラプラスの悪魔はその存在を否定されるしかないことになった。
一言いいたい!

【なにはさておき量子論 第3章 ハイゼンベルクの不確定性原理】
目次へ 次へ進む 前へ戻る


4.「粒子」と「波動」の意味
前期量子論とは何であったか?
そう、プランクが示したエネルギーの不連続。ボーアが証明した電子軌道の不連続。我々は、不連続なものを相手にしている、ということであった。ド・ブロイによって、電子波が発見され、それは、電子に限ったことではなく、あらゆる物質は、粒子と波動、両方の性質を持っていることも、示されたのだった。
ここに颯爽と登場したハイゼンベルクは、「不確定性原理」を言い出した。奇異に感じた人はいないだろうか?
前期量子論と不確定性原理には、何の関連があるの? それを今回は説明する。それは、「粒子」と「波動」の意味を理解することでもある。
不確定原理とは、
$\Delta{x}\times\Delta{p}\geqq h/4\pi$($h$はプランク定数)であった。
$\Delta{x}$は、位置の不確定の幅を示す。
$\Delta{p}$は、運動量の不確定の幅を示す。(速度の不確定と考えてもよい)
ここで、$\Delta{x}$を限りなく$0$に近づけてみよう。すると、
$\large{\Delta{p}\geqq \frac{h/4\pi}{\Delta{x}}}$なので、運動量の不確定の幅が無限大になる。すなわち速度がなくなってしまう。これは、運動量を問題にしなければ、位置だけははっきりする、ということだ。これまで私たちが考えていた古典粒子には位置がある。そして古典波動には、位置という概念はナンセンスである。(池に放り込んだ石が描く同心円状の波を考えてみればよい)
つまり、位置だけを確定させるということは、物質の粒子性を表現することになる。
これに対し、$\Delta{p}$を限りなく$0$に近づけてみる。
$\large{\Delta{x}\geqq \frac{h/4\pi}{\Delta{p}}}$なので、今度は、位置の幅が無限大になる。すなわち位置がなくなってしまう。これは位置を問題外として、運動量だけを考える、ということだ。位置のない運動量だけを決めるということは、それを波動と見たときの波長を決めてやることに相当する。(これは、ド・ブロイが発見した物質波に他ならない。〜$p=\frac{h}{\lambda}$)
よって、運動量だけを確定させるということは、物質の波動性を表現することになる。
よろしいか、つまり不確定性原理は、物質の究極の姿は、位置と運動量のどちらを正確に測るかによって、粒子だったり、波動だったりする、ということを言っている。
はい、プランク → ボーア → ハイゼンベルクとつながったね。
次に、($h/4\pi$)を考えてみよう。
もし、($h=0$)だったら、そもそも不確定性原理が意味を持たない。($\Delta{x}$)も($\Delta{p}$)もゼロでかまわない。従って、自然界は、連続であり、とびとびにはならない。
もし、($h/4\pi=100$)だったら、
$\Delta{x}=10$、$\Delta{p}=10$ということがあり得る。今単位を$\Delta{x}$を$m$(メートル)、$\Delta{p}$を($kg・m/$秒)とすると、なんと位置の不確定が$10m$、運動量の不確定が、$10kg・m/$秒である。もし物質の質量が$1kg$だったら、速度の不確定は$10m/$秒になる。これは、物質を「粒子」と「波動」の混合状態として見ることになってしまう。
もし、$1kg$の石が運動しているのを私たちが見たらどうなるか?
$0$〜$10m$の範囲にいることは、(なんとなく)わかる。という、なんだかわからないもうろうとしたものが、そこにある、ということになる。
$0$〜$10m/$秒の範囲で動いていることは、(なんとなく)わかる。
では、実際にはなぜこんなことになっていないか? それは、($h$)が非常に小さいからである。
再度、復習しておこう。($h$)をプランク定数といい、その値は、
$h=6.62607015{\times}10^{-34}$ $J$秒である。このように、プランク定数($h$)が、あまりにも小さい(当然、$h$を$4\pi$で割った数値は更に小さい)ので、$1kg$の石ころの不確定さなどとるに足らないものになる。だから、私たちは、石ころを、もうろうとしたもの、として見ることはないのだ。
相対論において、光速度が、私たちの日常の速度に対してあまりにも大きかったため、私たちは、相対論効果を日常で感じることはできなかった。
同様に、プランク定数が、私たちの日常物質の位置や速度に対して、あまりにも小さいので、私たちは、量子論効果を通常感じることはない。
例えば、さきほどの例で、$1kg$の石の位置を、$1mm$の$1000$分の$1$($1{\mu}m$:ほとんど私たちには見分けることができないほど小さい)の範囲で不確定であるとしても、その運動量は、$5.272859{\times}10^{-32}$$kg・m/$秒の範囲で不確定になっているはずで、こんな小さな速度のぶれなど、誰にもわからない。
でも、極微の世界では、そうは言っていられない。
電子の質量は、$9.1093897{\times}10^{-31}$ $kg$なので、いま電子の位置の不確定さ($\Delta{x}$)を、原子の大きさ程度とすると、
原子の大きさは、$10^{-10}$ $m$
\begin{equation} \large{ \Delta{p}=\frac{h/4\pi}{\Delta{x}}=\frac{6.6260755{\times}10^{-34}/4\pi}{10^{-10}}=5.272859{\times}10^{-25} \\ \Delta{v}=\frac{\Delta{p}}{9.1093897{\times}10^{-31}}=578837 m/秒 } \end{equation}となる。
意味のない計算をしていると思うだろうが、最後に出てきた速度($\Delta{v}$)は、実は、原子核の電荷がぎりぎり、電子をつなぎ止めておけるくらいの速度の不確定さなのである。
言い換えれば、原子の大きさより高い精度で電子の場所を確定させると、運動量の不確定さのため、電子は、原子から離れてどこかへ飛んで行く、ということになる。
つまり、電子は、原子の大きさ程度に位置が不確定でないと、原子の周りに存在できない。
なに、よく意味がわからん? 普通の人ならそれで正常。
電子は、原子の周りに存在する限り、原子の大きさ程度に位置が不確定になる、すなわち、電子は、原子核の周りに、まんべんなく存在しなければならない。よって、長岡半太郎が示した惑星モデルがここで破綻する。
電子は、原子核の周りに、もわーっと、雲のように存在することになる。
一言いいたい!

【なにはさておき量子論 第3章 ハイゼンベルクの不確定性原理】
目次へ 次へ進む 前へ戻る

チマローザ(の若い頃)
5.もう一つの不確定
ここまで、「なにはさておき量子論」を読み進めてくださった寛大なあなたにひとつ提案をする。
もし、「わかっても相対論」を読んでいないなら、ここで一旦、量子論を離れて、「わかっても相対論」を読んでいただきたい。全部とは言わない。第3章『質量はエネルギーである』まで、読破してもらいたい。なぜこんな提案をするかというと、「四元物理量」を知らない人が読んでも、この項がよくわからない恐れがあるからだ。いや、わかるように書いてもいいのだが、感動が薄れると言った方がいいかもしれない。
決断のできた方は、ここをクリック。
さて、ここにたどり着いたあなたは、四元物理量がなんであるかわかったとして、話を進める。
四元位置とは、何であったか?
$(ct,x,y,z)$であったはずである。 では、四元運動量は?
$(\frac{E}{c},p_x,p_y,p_z)$である。
さて、感動する準備はできたかな?
この四元物理量は、アインシュタインが「特殊相対性理論」の中で提唱したものである。それは、空間と時間を平等に扱ったら出てくる概念であった。従って量子論とは無関係のはずだ。私だってそれはわかっている。ところが面白いことが起こる。
前項までで書いた「位置と運動量の間には不確定の関係がある」を、四元物理量に中に見つけてみよう。
「位置」とは、空間上の場所である。前項までは代表して($\Delta{x}$)だけを書いてきたが、本来は
($\Delta{x},\Delta{y},\Delta{z}$)と表記するものだったのである。では運動量は? これも前項までは、($\Delta{p}$)で代表させて来たが、運動量はベクトルなので、方向成分を持つから、やはり($\Delta{p_x},\Delta{p_y},\Delta{p_z}$)と書くべきものであった。
よって、位置と運動量の不確定は、下記のように記述すべきものであった。
\begin{equation} \Delta{x}{\times}\Delta{p_x}\geqq h/4\pi \\ \Delta{y}{\times}\Delta{p_y}\geqq h/4\pi \\ \Delta{z}{\times}\Delta{p_z}\geqq h/4\pi \end{equation}これで空間部分の不確定性原理が、きちんと書けた。
では、四番目の物理量だって、不確定になるだろう、と考えてみたらどうなるか? 光速度($c$)は定数であるゆえ、
$c\Delta{t}{\times}\frac{\Delta{E}}{c}\geqq h/4\pi$が言える。なんと、四元物理量から、時間とエネルギーの不確定が出て来る。
$\Delta{t}{\times}\Delta{E}\geqq h/4\pi$
感動した?
これは、”チマローザ”が発見した。(わーい!私も量子論研究者の仲間入り。しかし当然、これが新発見であるわけもない。実は、位置と運動量、時間とエネルギーは「正準関係」にある、と言われ、量子論の計算(量子力学)では重要なものなのである。
本当は、次のような証明をするのが一般的。
今、自分胸あたりの深さの海の中に立って、波を見ているとする。波は、高い状態と低い状態があるから、一番低いときはへそのあたりで、高いときは首のあたりまで来るかもしれない。でもとにかく波がひと揺れしないことには、振動数($1$秒間に何回揺れるか)は、わからない。あたりまえ。この振動数を($\nu$)として、それを観測するのに必要な時間幅を($\Delta{t}$)とする。
$\Delta{t}=\frac{1}{\nu}$になることは、振動数の定義からわかりますね。
そして、第2章『ボーアの量子条件』の1.項『生みの親から育ての親へ』に出てきた
$E=h\nu$を考えれば
$\Delta{E}\geqq h/4\pi{\times}\frac{1}{\Delta{t}}$となる。
$\Delta{t}{\times}\Delta{E}\geqq h/4\pi$
さて、いったい時間とエネルギーの不確定って、いったいなんだろう。
一言いいたい!

【なにはさておき量子論 第3章 ハイゼンベルクの不確定性原理】
目次へ 次へ進む 前へ戻る

ゼノン
前項では、「時間」と「エネルギー」が不確定の関係にあることを見てきた。
この項ではその意味を考えてみよう。多分、前項を読んだだけでは、
$\Delta{t}{\times}\Delta{E}\geqq h/4\pi$の意味はわからないだろう。
まず最初に、エネルギーを確定させることを考えよう。
原子物理学では、エネルギーを正確に決めることが求められる。実は、今までにそんな話をいくつもしてきているのである。
例えば、水素原子から、光が飛びだして来る値が、光を粒子と考えると、バルマー系列やライマン系列のように、エネルギーがとびとびになる、ということが言えたのは、当然、エネルギーが確定していたからである。
 【再掲】
【再掲】エネルギーが確定していたということは、($\Delta{E}=0$)である(エネルギーの不確定要素がゼロなのだから)。ということは、不確定性原理を適用すれば、($\Delta{t}=\infty$)ということになる。さて、時間の不確定が無限大っていったい何?
簡単である。いつでも、エネルギーが確定しているということである。
これを、「定常状態」にある物質、という言い方をする。ある意味で、量子論の問題を解こうとするときには、対象物を「定常状態」である、としてエネルギーの方を決めてやることが多い。
では逆に、($\Delta{t}=0$)で、($\Delta{E}=\infty$)ということがあるか?
あるのだ。
極々、短時間($\Delta{t}\space{\fallingdotseq}\space0$)であれば、エネルギーの幅がとてつもなく大きく($\Delta{E}\space{\fallingdotseq}\space\infty$)なってもいいということだ。
($\space{\fallingdotseq}\space$)という歯切れの悪い記号を用いたことは許してもらいたい。私にも($\Delta{t}=0$)という状態(?)は想像できないのだ。ただ、次のようなことが考えられるだけである。
ちょっと寄り道をする。
($\Delta{t}=0$)は、『文学的』に言う「ある瞬間」というものと同義である。なぜ『文学的』かって? だって『物理的』に想像できないんだもの。なんとなく、全てのものが止まった世界を考えることができるだけである。そうであるとすれば、その『文学的』世界では、多分($\Delta{x}=0$)が言える。つまり、あらゆる物質が静止した世界だ。
いかなるものも動いていない。動いていないものに対して速度(どちらの方向へどのくらいの速さで動いているか)が定義できるか? 速度の定義から言って自己矛盾だろう。だってその物体は動いていないのだから。
「”ゼノン”のパラドックス」というのを知っているだろうか? 実はふたつあるのだが、今回はそのひとつを紹介する。(と言っても多分みなさんご存じだろう。)それは、「飛んでいる矢は止まっている」というものだ。
(1)放たれた矢が、$100m$を飛んで行くことを考える。どこまでも続けて書くことができる。上記より、「放たれた矢は、放たれた点から先に進むことができない $=$ 飛んでいる矢は止まっている」というパラドックスである。
(2)放たれた矢は、$50m$地点まで行かなければ$100m$飛ぶことはできない。
(3)放たれた矢は、$25m$地点まで行かなければ$50m$飛ぶことはできない。
(4)放たれた矢は、$12.5m$地点まで行かなければ$25m$飛ぶことはできない。
(5)・・・
さあ、どう解決する?(ちなみにゼノンが考えたもうひとつのパラドックスを「アキレスと亀」のパラドックスという。こっちの方が有名かな? 「アキレスと亀」の話は、『問わず語り』にアップしている。)
つまり極限まで突き詰めると、静止してしまう物質はないのだ。粒子の位置($\Delta x$)を限りなくゼロに近づけても、矢は、運動量($\Delta p$)を持つ。点ではなく、何となく進行方向に少し延びている(ように私は思う)。
だから、「位置」と「運動量」の不確定は、「時間」と「エネルギー」の不確定と同じだ(と私は考えている)。直感的には、このように言った方がわかりやすいと思う。
「真空の揺らぎ」という現象がある。ある、と言い切るところから話をはじめると本当はルール違反である。
なのでこう書く。
極々短い時間なら、大きなエネルギーが生まれてもよい。以上を「真空の揺らぎ」という。
よって、エネルギーが生まれる。
質量はエネルギーである。
よって、エネルギーから、質量が現れてもよい。
しかし、極々短い時間内で、その質量は消えてしまわなければならない。
よって、生まれるのは、「物質」と「反物質」である。
生まれて、極々短い時間内で、「物質」「反物質」は消滅し、エネルギーに戻る。
エネルギーは、極々短い時間内に消える。
つまり真空という、一見何もない空間でも、極々短い時間では、物質(と反物質)が生まれては消える、という現象があらゆる場所で起こってもよい。「真空の揺らぎ」によって、発生している(であろう)物質を、「仮想粒子」という。
ここで、次の疑問を持った人はいないだろうか?
物理学は、人間が認識できないものを相手にしないはずではなかったか? 鋭い。これを言える人は、トレビヤン!
ところが、「仮想粒子」が仮想でなくなることがあるのだ。
次章へ 一言いいたい!
